This article is outdated and to be updated
Site Construction Info

Resonant Iris Filter

What is a quarter-wave-coupled filter

A quarter-wave-coupled filter consists of independent resonators coupled with each other by a transmission line sections of 90 dg. phase length. Independence of the resonators means that each of those resonators is matched with the transmission line and shows some resonant behavior. By the rule it should have at least one reflection zero in the design bandwidth. Each resonator can be characterized by two parameters such as central frequency ( fo ) and quality factor ( Q ). The central frequency , fo is the location of reflection zero. The quality factor, Q can be defined by different ways. Here it is determined by reflection slope in the vicinity of fo (see Technical Notes). Technical realization of such type of filters can be different, but here only classic resonant iris filter is considered.


What is the resonant iris

A resonant iris can be a metallic window extending across the both waveguide dimensions. The iris can be considered as a section of smaller waveguide with the cut-off frequency being close to fo. In this case the iris can provide zero of reflection at fo. Practical realization of such an iris can be a small rectangular diaphragm with width close to 1/2 cut-off wavelength.



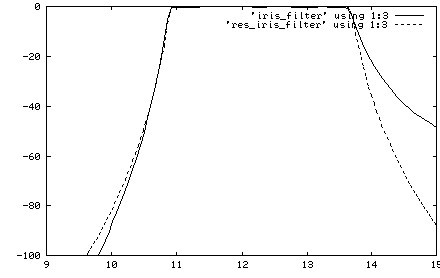
Figure 1: Transmission response of two 11-pole chebychev filters using H-plane and resonant irises.
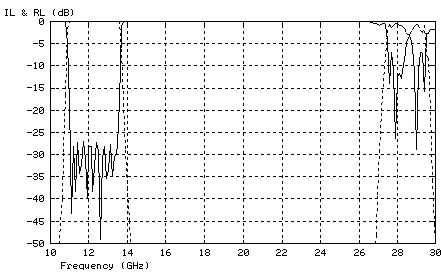
Figure 2: High spectrum isolation of a Ku-band 11-pole resonant iris filter.

Where the resonant iris filter is better than a regular iris filter

Any filter built from H-plane irises or posts shows less isolation on right roll-off than on left side. This is a characteristic of a regular iris or post filter which much reduces its trade-off value. The resonant iris filter can provide a symmetric frequency response (see Figure 1) as well as with more lower isolation or more upper isolation. This property of response is adjustable by distance between irises. Also the length of a resonant iris filter can be twice smaller than the appropriate iris or post filter providing the same isolation and bandwidth. For example, the resonant iris filter with response shown on Figure 1 is not longer than 2 inches but its regular iris analog is 5.5 inches long, though the both filters provide 11-pole frequency response.


Where the resonant iris filter is better than a corrugated or ridged filter

Sometimes a resonant iris filter can replace a cascade of an iris filter and corrugated or ridged filter as it can provide a wide stop-band and a symmetric sharp roll-off. As a regular corrugated filter, it has some spurious harmonic pass bands. This pass-bands can appear when the coupling space between irises becomes multiple to 1/2 wavelength in the waveguide or at the frequencies of high order resonance of the irises. Commonly the resonant iris filter is not able to provide 3rd harmonic requirements. However, it can be a better solution to cover a band from near pass-band to the 2nd harmonic, as it is smaller.


Where the resonant iris filter is better than a dual mode filter

The internal structure of a resonant iris filter can be even shorter than a dual mode filter of the same order. Also it can cover so wide frequency range ( 20% and more) and reject remote frequencies what a dual mode iris filter cannot.




Why the resonant iris filters are hardly used in waveguide applications if they are so good?

Mostly because of two following important demerits:
1. High insertion loss. Insertion loss of a resonant iris filter is usually higher than insertion loss of regular iris filter of the same bandwidth and order.
2. Low peak power handling. Vacuum or air breakdown power level is lower in comparison with an equivalent H-iris filter.