---

Spurious Pass-Bands of Corrugated Filter

As corrugated filters are based on two-dimensional structure, the frequency response of any waveguide mode propagating in E-plane structure is of same first index is a function of only b (propagation number). Therefore frequency responses of TE_N0-mode show similarity to the frequency response of the dominant TE₁₀-mode including its stop-bands as well as its pass-bands. Generally existence of the pass-bands of high order modes does not necessary mean the filter cannot reject the frequency spectrum corresponding to those spurious pass-bands. Actual filter performance depends on what kinds of modes are carrying the spectrum. For example, measured between two waveguide-to-coaxial transitions, the filter may demonstrate solid rejection up to second harmonic and even higher because the spurious modes are not excited by setup components (See Fig 1). However, the "bad" modes might be excited in the real system where the corrugated is intended to be used (see Fig 2).

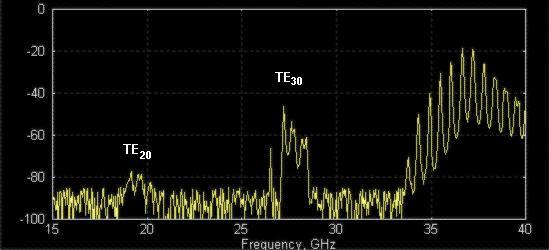
Figure 1: Transmission response measured using “regular” (symmetric) calibration. TE-mode level is low because measurement components and filter are symmetric. TE20-mode level is higher because it is excited by transformer steps of filter.

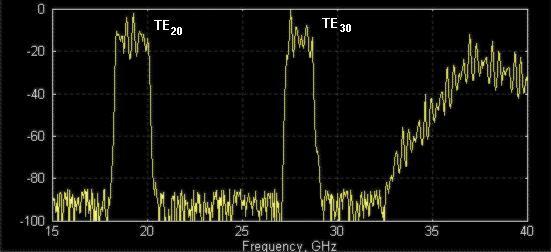
Figure 2: Transmission response measured using “exciters” of higher order modes (regular setup components do not excite them much). The both TE20- and TE30-modes popped up, because not rejected by filter.

As the modes composition of the macro system is unknown, it is better to assume the worst case of existence of all the bad modes. Generally there is no way eliminate the spurious pass-bands for a corrugated filter except moving them out of the important frequency bands. The positions of pass-bands of spurious modes depend on pass-band of the dominant mode and the width of corrugated waveguide. Therefore it is a good idea to locate bands with potential lack of rejection in respect to rejection requirements. The picture shown on Fig 3 tells how to predict pass-bands of spurious modes using the first design step page.

Figure 3: Example of selection width of corrugated waveguide and cut-off point.

Synthesis of Initial Dimensions

If the “spurious” width is determined, other dimensions of corrugated filter can be obtained by following simple procedure. The design procedure presented here differs from conventional design procedures based on direct synthesis of filter dimensions using equivalent circuit networks and special functions or polynomials. The conventional procedures are found to be practically ineffective because they make accent on pass-band performance rather than higher stop-band where the prototype networks do not model electromagnetic propagation in waveguide structures. Therefore the design procedure used here is based on selection of prototypes of good upper stop-band rejection and bad pass-band performance and further optimization of pass-band. There are two types of prototypes used here. Prototype [option 1] is preferable if end frequency point of upper stop-band is less than 2.5-3 times central frequency of the filter pass-band. The option #1 provides better initial pass-band performance and therefore is easier to design. The prototype [option 2] is preferable to reject frequency spectrum up to 3-4 times of central frequency of the pass-band. Since you have entered roll-off and width of corrugations in the first design page, the synthesizer will try to find optimal values for Bmin and Bmax values, the network parameters of prototype.

Figure 4: Key dimensions of corrugated structure to be specified in order to generate initial (draft) design.

Therefore click button [Generate Dimensions] and go to next design page by clicking button [Simulate Response] in order to simulate frequency response there (see Fig 5).

Figure 5: Control panel.

Corrugated Filter Simulator

This is a stand-alone verification tool. If you have already obtained initial dimensions in previous design page, those dimensions will be automatically transferred to the simulator. You may correct them or replace them with other design, as the program module is independent from other design steps. In order to simulate filter performance click button [Simulate] (see Fig 6).

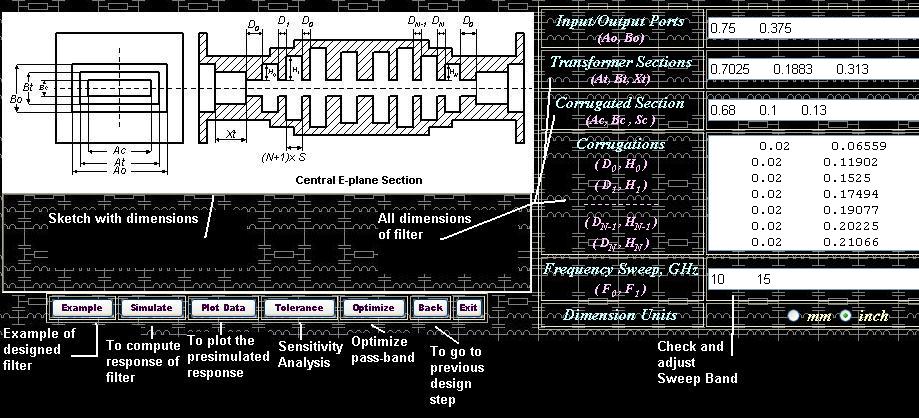
Figure 6: Appearance of interface of the Simulator.

The process of simulation can take not more than 1-2 seconds for Pentium 4 computer. For slower computers a warning note shown on Fig 7 can appear during simulation. The message means IE is unresponsive during computation, i.e. does not respond on other events like mouse clicking or resizing windows. The Simulator and some other design tools of my Design Studio are based on “client side” VBScripts, but scripts usually take full control over browser while running. The browser (Internet Explorer) is not designed as a computational tool, so its computational efficiency and operational memory are very low. Therefore it is recommended to cancel all other windows jobs and wait until computation completed and [Simulate] button is released. After simulation is completed and browser became responsive, you can see plot of simulated frequency response of filter by pressing the next button [Plot Data].

Figure 7: A warning note may appear. The note warns that during simulation time [if it is more than couple of seconds] Internet Explorer may become unresponsive [will not act other events like mouse clicking, windows switching, resizing, etc.]. Click [Yes], if you want cancel simulations. Click [No] if you want to continue simulation. If you run simulations, please do not try to execute other commands or events until all computations are completed.

Response Plotter

If you press [Plot] button, you can see plot of reflection and transmission in dB vs. frequency. Please do not expect performance of initial design to be great. The picture below (see Fig 8) shows how it usually looks like.

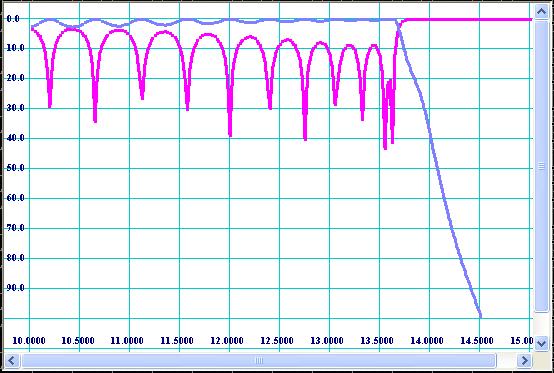
Figure 8: Typical reflection and transmission performance of “draft” design.

Check position of bandwidth and cut-off (roll-off) in accordance with your spec. If your spec do not contain requirements for lower (roll-off) rejection (only harmonics), you have to specify the filter roll-off anyway as design reference point because it effects bandwidth of spurious modes (see Fig 1). You can correct bandwidth by repeating the second design step, i.e. slightly changing Bmin and Bmax values of prototype and re-synthesizing the dimensions. Simultaneously it is recommended to check rejection of higher frequency spectrum (harmonics). If rejection is not adequate, more corrugations are needed. Actually all initial parameters effect on potential performance of the filter and there is no single recommendation how to design the best filter. That is not like designing waveguide iris filter when filter bandwidth and order are only parameters. This procedure is not unambiguously determined, i.e. they might be different types of corrugated filters matching the same spec. Therefore, you may try different initial parameters and subsequently compute frequency response until you are satisfied with dimensions and rejection (not pass-band) performance of the draft design.

Response Optimizer

No customer indeed will be happy with a harmonic filter having such an ugly pass-band performance shown on Fig 8. Therefore the design is not completed until the reflection ripples of the filter pass-band are not reasonably small. Therefore we need an optimizing tool in order to improve the performance of filter pass-band. Although pass-band performance of “draft” design is so low, it might need some slight adjustment of corrugations and transformer steps in order to make it much better. Optimizer is a tool, which runs various combinations of dimensions and computes the path of improvement (gradient) of a function of performance (functional). Therefore it is important to specify optimization goals and limits (constrains) effectively in order to achieve the best performance. Example of selection of optimization constrains is shown on Fig 9.

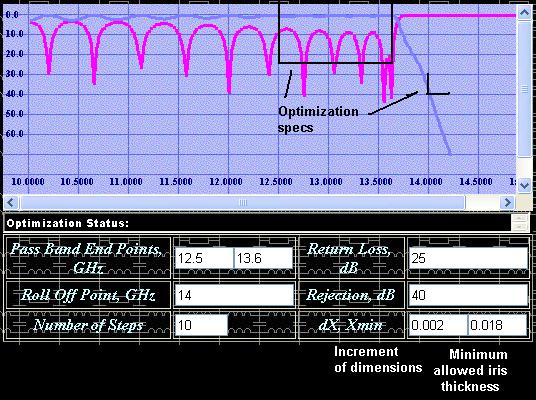
Figure 9: Selection of optimization constrains.

The optimization constrains have to be reasonable. For example, do not try to make filter wider than you really need or optimize rejection of harmonics. The optimizer is based on gradient method, which is good only for finding “local” minimums, i.e. slight improvement. While optimizer is running, the filter dimensions are changing. Over optimization may worsen other parameters of filter as length and rejection of higher frequencies. Therefore, periodically check transmission response over wide frequency sweep. The optimization increment dX is the change of any of dimensions (thickness of irises, depth of cavities, transformer length and width) during one step of optimization. Initially the value of dX may be selected as 0.002-0.004 times of the interface waveguide width. While the reflection ripple is reducing, the increment has to be reduced up to ten times (0.0002-0.0004 times interface width). Sometimes some of the dimensions (irises between corrugations) might tend to unrealistic and even negative values. Therefore you might need to specify the minimum thickness of irises, for example 0.018’’-0.022’’. While optimizing, the bandwidth of filter can move along the frequency axis. You can slightly move the bandwidth using appropriate button (see Fig 10). If the button [Adjust Band] is clicked, a window with input line will appear. Enter a value slightly less than 1 in order to reduce frequency plan and a value slightly greater than 1 in order to move the frequency plan forward the frequency axis (increase).

Figure 10: Control panel of the Response Optimizer.

The same precautions have to be taken into account while using the optimizing tool. The optimizer is based on the same type of VBScript code and is not responsive while running. Please read warning notes marked red and written above and below the Fig 7. Optimization process may require from 40 to 100 optimization steps and from 15 to 45 minutes for an experienced designer. At the end of optimization the pass-band frequency response of filter should be much better (see Fig 11).

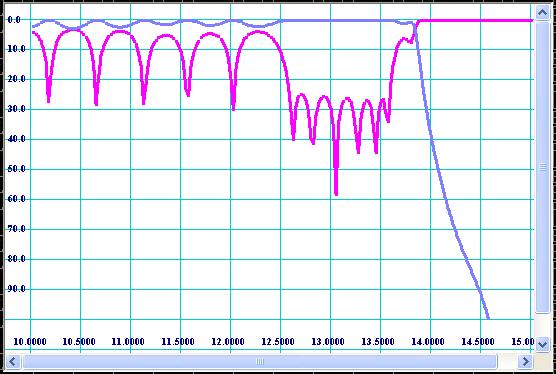
Figure 11: Frequency response of optimized filter.

Frequency response of “optimized” filters might not be so “esthetically beautiful” as Chebychev, Zolotarev and other polynomials look like, but it can be really “optimal” in respect to formal specs. For example, size, manufacturability, power handling and harmonics rejection are not involved into conventional synthesis methods, but they are the most valuable features of harmonic filters. The main advantage of optimization design methods over the direct synthesis ones is flexibility and trade offs.

Final Revision

During and after optimization the filter has to be virtually tested over wide frequency sweep for spikes and zones of lack of rejection. The Fig 12 shows wide sweep frequency transmission response for the optimized design.

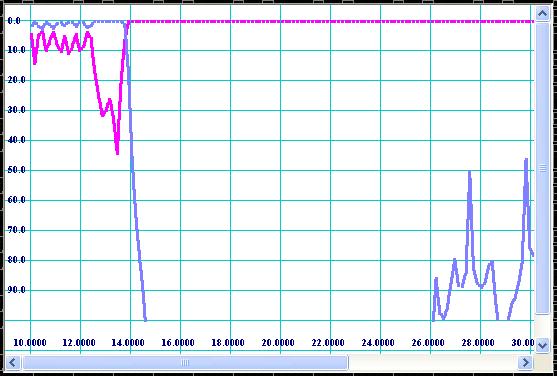
Figure 12: Response over wide frequency sweep.

It should be noticed that the response obtained by simulation over high frequency spectrum corresponds to TE10-mode transmission and reflection only. It is recommended to check the responses of spurious modes also. In order to do so, simply replace internal width of corrugations (see Fig 6) by Ac/2 value for TE20-mode, Ac/3 for TE30-mode, Ac/4 for TE40-mode, etc and compute frequency response. For our example, values 0.34 (0.68/2) and 0.2267 (0.68/3) are entered for modes of TE20 and TE30 respectively and plots shown on Fig 13 and Fig 14 are obtained.

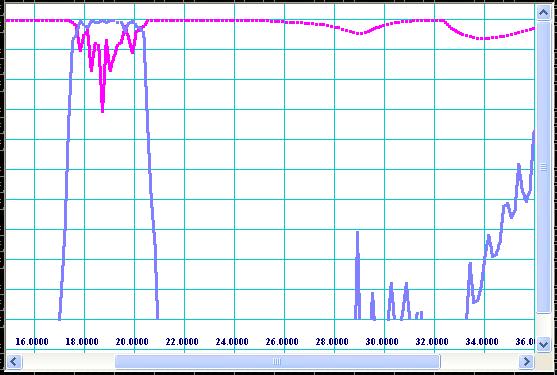
Figure 13: Plot of TE20-mode frequency response.

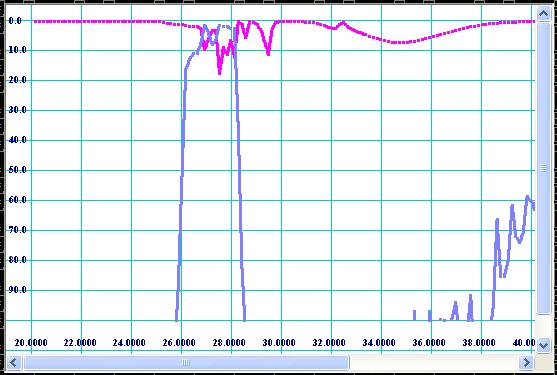
Figure 14: Plot of TE30-mode frequency response.

As it is mentioned above, the plots correspond to the worst case of propagation of the spurious modes, if they are excited for 100%. Practically they might be hardly noticed (as showed on Fig 1) and be reason of mysterious and unsolvable “quality” problems further. Therefore is better to double check the spurious positions during design process by such a simple trick.

Sensitivity Analysis

As it is practically impossible to produce hardware with dimensions identically equal to the dimensions assumed to be optimal (designed) because of inaccuracy of real production methods, it is at least useful to know what kind of performance the reality hardware would demonstrate. Different production methods such as EDM, milling, casting, galvanic forming, water jets, and others have their characteristic tolerances. In conformity with corrugated filters the most popular production methods can be specified by rounding of straight corners and deviation of positions of vertexes of cavities. The both effects may be evaluated by Sensitivity Analyzer linked to the Simulator by [Tolerance] button. Four types of manufacturing tolerances are specified there. H-plane milling tool radius is radius of milling cutter applied to corrugation on H-plane, i.e. if the filter is composed from two half bodies to be connected on central H-plane by flanges. H-plane assembling is easier to produce by milling, but it is less reliable than E-plane assembling because potential flange contact problems. Although E-plane assembling has a big advantage such as insensitivity for flange contact quality, it is seldom used because it is larger than H-plane one, more sensitive for cavity rounding and it requires deeper penetration of cutter (larger cutter is required). EDM is very accurate, so tolerances and radii are negligible small. However it is expensive and therefore production people do not like to use it for mass production. Galvanic forming has advantage over “machine” methods, as it can build filter as monolithic unit with no contact flanges. However galvanic methods are less accurate and have environmental problems. It is direct responsibility of design engineer to provide sensitivity analysis over possible production methods in order to eliminate potential quality assurance problems. For example the frequency response shown on Fig 11 may degrade to the response shown on Fig 15, if reasonable production errors are applied (radius of milling tool is 0.064’’ and random tolerances are +/- 0.0005’’). Nevertheless, the “example” filter (press [Example] option of Simulator) shows much less degradation of frequency response caused by the same production tolerances.

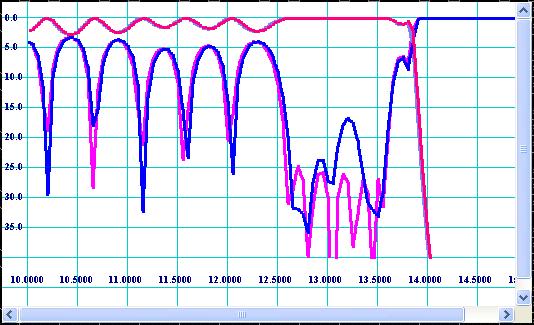
Figure 15: Degradation of frequency response shown on Fig 11 caused by milling tolerances.

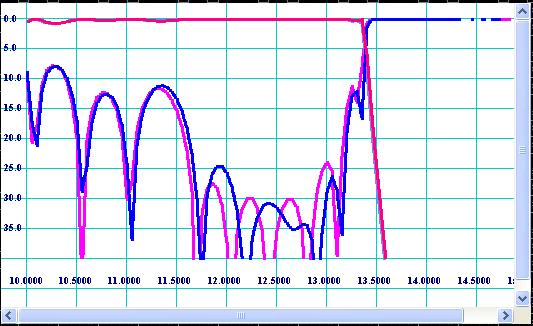
Figure 16: Degradation of frequency response of “example” filter caused by same milling tolerances.

Nevertheless in accordance with sensitivity analysis the bad filter may be produced using EDM method because EDM tolerances impact is more or less acceptable (see Fig 17).

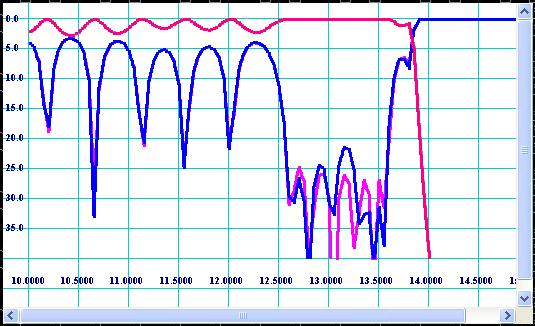
Figure 17: Degradation of frequency response shown on Fig 11 caused by EDM tolerances.

The analysis shows that the “example” filter is stable for production errors and can be produced by “cheap” production methods. The other filter should be produced by only accurate production methods and might be expensive. Stability for production tolerances depends on many design factors such as equivalent values and distribution of discontinuities along the filter structure. Usually filters having wider design pass-band are more stable. I have found some types of corrugated structures, for example quarter-wave-coupled, being also more forgiving the production errors.

Accuracy

There is very strong and very wrong believe among engineers that “accurate EM based” software, for example HFSS, is more accurate because licenses are expensive. Contradictory, they think my Design Studio must be very inaccurate only because it is a free online toy. I can claim that my Design Studio is more accurate and hundreds of times faster than, for example, HFSS because it is based on analytically pre-solved problems of scattering and propagation in real (non-discrete) space. Practically the software accuracy is more sophisticated. None of existing EM simulation tools can be called as “accurate” because no exact solutions of corresponding Maxwell equations within appropriate “practical” boundary conditions have been found. All numerical methods ever been developed are approximate. The accuracy problem is based on convergence problem, which is based on idea that “for any ε >0 there always exist N, so for any n>N |An-A| < ε”. None of existing EM numerical methods is approved over the convergence criterion by mathematicians. Therefore “to converge or not to converge” is still the question. So no trust to any simulation results should be given. Some of simulation tools providers can argue this my point of view, but I am quite sure no one would take my engineering responsibility for failure of “well pre-simulated” designs. Therefore, I cannot also guarantee my Design Studio is an “exact” design tool. However, I assume my Simulator provides “practical” accuracy, i.e. slight shift of bandwidth and return loss deviation for “design stable for errors” (see rubric above) in respect to “reality”. Stability for errors is something associated with design itself rather than with software. As computational errors make similar effects for filter simulation results as production errors, the designs stable for tolerances should be more “simulatable”.

TO BE CONTINUED